Practicing graphical debugging using too many visualizations of the Hilbert curve
“..you don't understand things, you just get used to them.”— John von Neumann
For a while now I've been advocating for a particular style of programming:
- Use tools that don't change too often.
- Use tools that don't keep historical accidents around indefinitely.
- Minimize moving parts. Avoid additional third-party libraries, and forswear native libraries entirely.
Lua and LÖVE have been one nice way to get these properties. As I've used them, I've enjoyed an additional benefit: the ubiquitous presence of a canvas I can draw on as I program. This has been new to me with my erstwhile conservative and terminal-bound habits, and I've been pushing myself to lean more on graphics to understand what my programs are doing. Here I want to share one such experience. I'm using my run-anywhere Lua Carousel app, and you can paste the programs directly into it, but the workflow translates to any platform with a canvas.
A few weeks ago Jack Rusher shared a baffling function to compute the Hilbert curve. Here it is, translated to Lua:
function h(x, y, xi, yi, xj, yj, n) if n <= 0 then return {x+xi/2+xj/2, y+yi/2+yj/2} end return array_join( h(x, y, xj/2, yj/2, xi/2, yi/2, n-1), h(x+xi/2, y+yi/2, xi/2, yi/2, xj/2, yj/2, n-1), h(x+xi/2+xj/2, y+yi/2+yj/2, xi/2, yi/2, xj/2, yj/2, n-1), h(x+xi/2+xj, y+yi/2+yj, -xj/2, -yj/2, -xi/2, -yi/2, n-1)) end
When I first looked at it, I could see a few superficial facts:
- It returns an array of points containing x and y coordinates.
- It's recursive. There's a base case for “leaf” calls, and each non-base case makes 4 recursive calls.
- Only the base case actually “draws” by adding points to the result.
- Non-leaf calls recursively partition the given square into 4 quadrants. Square size (the xi/yi/xj/yj) is being halved each time.
v1: The first thing to look at is the curve itself.

code
function h(x, y, xi, yi, xj, yj, n)
if n <= 0 then
return {x+xi/2+xj/2, y+yi/2+yj/2}
end
return array_join(
h(x, y, xj/2, yj/2, xi/2, yi/2, n-1),
h(x+xi/2, y+yi/2, xi/2, yi/2, xj/2, yj/2, n-1),
h(x+xi/2+xj/2, y+yi/2+yj/2, xi/2, yi/2, xj/2, yj/2, n-1),
h(x+xi/2+xj, y+yi/2+yj, -xj/2, -yj/2, -xi/2, -yi/2, n-1))
end
function array_join(...)
local result = {}
for i, arg in ipairs{...} do
for _,x in ipairs(arg) do
table.insert(result, x)
end end
return result
end
local pts = h(60, 60, 800, 0, 0, 800, 5)
function car.draw()
color(0,0,1)
line(unpack(pts))
end
This uses some abbreviations from Lua Carousel. We save the list of points and draw them as a polyline.
Compare the L-system based implementation on Wikipedia:
code
function lsys(s)
local result = {}
for i=1,#s do
local c = s:sub(i,i)
if c == 'A' then
table.insert(result, '+BF-AFA-FB+')
elseif c == 'B' then
table.insert(result, '-AF+BFB+FA-')
else
table.insert(result, c)
end
end
return table.concat(result)
end
function draw_lsys(s)
for i=1,#s do
local c = s:sub(i,i)
if c == 'F' then
forward()
elseif c == '+' then
left()
elseif c == '-' then
right()
end end end
function forward()
local x2 = x+dirx*n
local y2 = y+diry*n
line(x,y, x2,y2)
x,y = x2,y2
end
function left()
if dirx == 0 then
dirx = diry
diry = 0
else
diry = -dirx
dirx = 0
end end
function right()
if dirx == 0 then
dirx = -diry
diry = 0
else
diry = dirx
dirx = 0
end end
x,y = 100,100
dirx,diry = 0,1
n = 10
g.setLineWidth(3)
color(1,0,1, 0.1)
s = 'A'
for _ = 1,5 do
s = lsys(s)
end
draw_lsys(s)
How does it work?!
v2: Print out the sequence of calls in Jack's program.
code
function h(x, y, xi, yi, xj, yj, n)
print(x,y, xi,yi, xj,yj)
if n <= 0 then
return {{x=x+xi/2+xj/2, y=y+yi/2+yj/2}}
end
return array_join(
h(x, y, xj/2, yj/2, xi/2, yi/2, n-1),
h(x+xi/2, y+yi/2, xi/2, yi/2, xj/2, yj/2, n-1),
h(x+xi/2+xj/2, y+yi/2+yj/2, xi/2, yi/2, xj/2, yj/2, n-1),
h(x+xi/2+xj, y+yi/2+yj, -xj/2, -yj/2, -xi/2, -yi/2, n-1))
end
function array_join(...)
local result = {}
for i, arg in ipairs{...} do
for _,x in ipairs(arg) do
table.insert(result, x)
end end
return result
end
h(0,0, 800,0, 0,800, 2)
To keep the output manageable, we'll look at just a second order Hilbert curve
(so the final n input is 2).
Running this results in the following output.
60 60 800 0 0 800
60 60 0 400 400 0
60 60 200 0 0 200
60 260 0 200 200 0
260 260 0 200 200 0
460 260 -200 -0 -0 -200
460 60 400 0 0 400
460 60 0 200 200 0
660 60 200 0 0 200
660 260 200 0 0 200
660 460 -0 -200 -200 -0
460 460 400 0 0 400
460 460 0 200 200 0
660 460 200 0 0 200
660 660 200 0 0 200
660 860 -0 -200 -200 -0
460 860 -0 -400 -400 -0
460 860 -200 -0 -0 -200
460 660 -0 -200 -200 -0
260 660 -0 -200 -200 -0
60 660 200 0 0 200
Looking at this, some facts are clear without needing to think too hard:
- xi/yi and xj/yj are axis-aligned. One of each pair is always 0.
- Exactly one of each pair xi/xj and yi/yj is 0. That explains why the above code sometimes adds both.
v3: Let's look at Jack's original animation.
code
function h(x, y, xi, yi, xj, yj, n)
if n <= 0 then
return {{x=x+xi/2+xj/2, y=y+yi/2+yj/2}}
end
return array_join(
h(x, y, xj/2, yj/2, xi/2, yi/2, n-1),
h(x+xi/2, y+yi/2, xi/2, yi/2, xj/2, yj/2, n-1),
h(x+xi/2+xj/2, y+yi/2+yj/2, xi/2, yi/2, xj/2, yj/2, n-1),
h(x+xi/2+xj, y+yi/2+yj, -xj/2, -yj/2, -xi/2, -yi/2, n-1))
end
function array_join(...)
local result = {}
for i, arg in ipairs{...} do
for _,x in ipairs(arg) do
table.insert(result, x)
end end
return result
end
local pts = h(60, 60, 800, 0, 0, 800, 5)
local curr_index = 0
local speed = 100
function car.draw()
color(0,0,0)
for i=2,curr_index do
color(0,0,0)
line(pts[i-1].x, pts[i-1].y, pts[i].x, pts[i].y)
end
end
function car.update(dt)
curr_index = curr_index + dt*speed
if curr_index > #pts then curr_index = #pts end
end
It shows the order in which leaf calls are computed, but that path is pretty complicated.
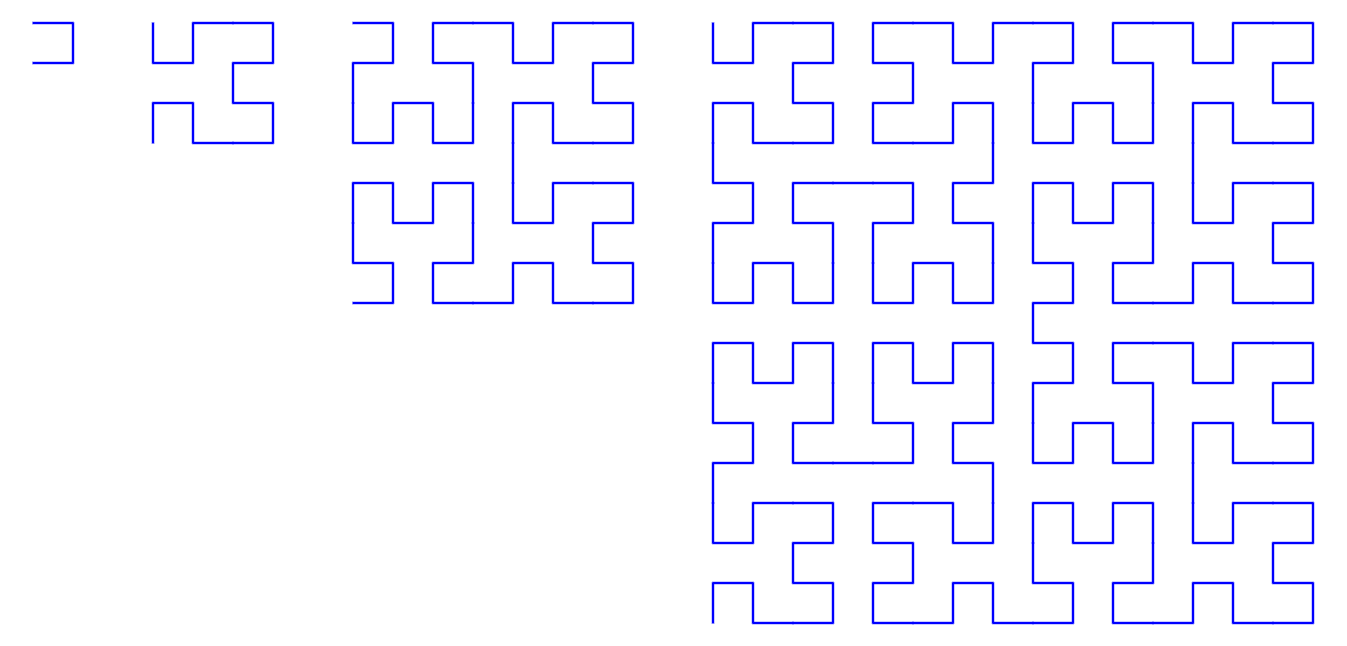
v4: Maybe it'll help to see a few iterations next to each other.
code
function h(x, y, xi, yi, xj, yj, n)
if n <= 0 then
return {{x=x+xi/2+xj/2, y=y+yi/2+yj/2}}
end
return array_join(
h(x, y, xj/2, yj/2, xi/2, yi/2, n-1),
h(x+xi/2, y+yi/2, xi/2, yi/2, xj/2, yj/2, n-1),
h(x+xi/2+xj/2, y+yi/2+yj/2, xi/2, yi/2, xj/2, yj/2, n-1),
h(x+xi/2+xj, y+yi/2+yj, -xj/2, -yj/2, -xi/2, -yi/2, n-1))
end
function initialize_curves()
local pts = {}
local side = 80
local x, y = 60, 60
for n=1,4 do
table.insert(pts, h(x,y, side,0, 0,side, n))
x = x + side + 40
side = side*2
end
return pts
end
local pts = initialize_curves()
function car.draw()
color(0,0,1)
for _, pts in ipairs(pts) do
draw_lines(pts)
end end
function draw_lines(pts)
for i=2,#pts do
line(pts[i-1].x, pts[i-1].y, pts[i].x, pts[i].y)
end end
Hmm, not so much. It's helpful to see the first iteration in particular. 4 calls yield 4 points, which string together into 3 lines that don't quite complete a square. But beyond that, it's still murky.
v5: As I said, only the leaf calls actually add any points. What if we show more details for each of them? Each leaf call uses 3 points on the way to adding one point to the result.

code
function h(x, y, xi, yi, xj, yj, n)
if n <= 0 then
local resultx, resulty = x+xi/2+xj/2, y+yi/2+yj/2
local x3, y3 = x+xi, y+yi
local x4, y4 = x+xj, y+yj
local debug = {
{type='circle', drawmode='fill', x=x, y=y, radius=2, r=1,g=0,b=0},
{type='line', x1=resultx, y1=resulty, x2=x, y2=y, r=1,g=0.5,b=0.5},
{type='circle', drawmode='line', x=x3, y=y3, radius=5, r=0, g=1, b=0},
{type='line', x1=resultx, y1=resulty, x2=x3, y2=y3, r=0.5,g=1,b=0.5},
{type='circle', drawmode='line', x=x4, y=y4, radius=5, r=0, g=1, b=0},
{type='line', x1=resultx, y1=resulty, x2=x4, y2=y4, r=0.5,g=1,b=0.5},
}
return {{x = resultx, y = resulty, draw=debug}}
end
return array_join(
h(x, y, xj/2, yj/2, xi/2, yi/2, n-1),
h(x+xi/2, y+yi/2, xi/2, yi/2, xj/2, yj/2, n-1),
h(x+xi/2+xj/2, y+yi/2+yj/2, xi/2, yi/2, xj/2, yj/2, n-1),
h(x+xi/2+xj, y+yi/2+yj, -xj/2, -yj/2, -xi/2, -yi/2, n-1))
end
function array_join(...)
local result = {}
for i, arg in ipairs{...} do
for _,x in ipairs(arg) do
table.insert(result, x)
end end
return result
end
function initialize_curves()
local pts = {}
local side = 80
local x, y = 60, 60
for n=1,4 do
table.insert(pts, h(x,y, side,0, 0,side, n))
x = x + side + 40
side = side*2
end
return pts
end
local pts = initialize_curves()
function draw_hilbert(pts)
color(0,0,1)
g.setLineWidth(2)
for i=2,#pts do
line(pts[i-1].x, pts[i-1].y, pts[i].x, pts[i].y)
end
for _, pt in ipairs(pts) do
if pt.draw then
for _,shape in ipairs(pt.draw) do
color(shape.r, shape.g, shape.b, shape.a)
if shape.type == 'circle' then
circle(shape.drawmode, shape.x, shape.y, shape.radius)
elseif shape.type == 'line' then
line(shape.x1, shape.y1, shape.x2, shape.y2)
end end end end
end
function car.draw()
for _, pts in ipairs(pts) do
draw_hilbert(pts)
end end
This is pretty. Every point can now contain a bag of debug data, commands to draw additional shapes. Since xi, yi, xj, yj are all distances not positions, I'm plotting (x+xi, y+yi) and (x+xj, y+yj), and it becomes obvious how the 3 points collaborate to form each point on the Hilbert curve. It becomes apparent that the control points are always oriented north-west to south-east, translating the base point (x, y) along a north-east to south-west orientation (the red lines).
But what's the pattern beyond that orientation? There's still more to dig here.
v6: Perhaps it would help to look at the scaffolding. Instead of showing me how the three points form the fourth, show me the “envelope” for each recursive call.

code
local ox,oy = 300,100 -- where to start drawing
local N = 800 -- size of the drawing
local depth = 4 -- levels of recursion; 0 = single point
-- colors
local primary = {r=1, g=0.8, b=0}
local control = {r=0, g=0.8, b=0.8}
local c = 0.8
local scaffold = {r=c, g=c, b=c}
function h(x, y, xi, yi, xj, yj, n, N)
if N == nil then N = n end
local x3, y3 = x+xi, y+yi
local x4, y4 = x+xj, y+yj
if n <= 0 then
local resultx, resulty = x+xi/2+yi/2, y+yi/2+yj/2
local debug = {
{type='circle', drawmode='fill', x=x, y=y, radius=5, color=primary},
{type='line', x1=resultx, y1=resulty, x2=x, y2=y, color=primary},
{type='circle', drawmode='line', x=x3, y=y3, radius=10, color=control},
{type='line', x1=resultx, y1=resulty, x2=x3, y2=y3, color=control},
{type='circle', drawmode='line', x=x4, y=y4, radius=10, color=control},
{type='line', x1=resultx, y1=resulty, x2=x4, y2=y4, color=control},
}
return {{x = resultx, y = resulty, draw=debug}}
end
local result = array_join(
h(x, y, xj/2, yj/2, xi/2, yi/2, n-1, N),
h(x+xi/2, y+yi/2, xi/2, yi/2, xj/2, yj/2, n-1, N),
h(x+xi/2+xj/2, y+yi/2+yj/2, xi/2, yi/2, xj/2, yj/2, n-1, N),
h(x+xi/2+xj, y+yi/2+yj, -xj/2, -yj/2, -xi/2, -yi/2, n-1, N))
if result[1].draw == nil then result[1].draw = {} end
result[1].draw = array_join(result[1].draw, {
{type='line', x1=x, y1=y, x2=x3, y2=y3, color=scaffold},
{type='line', x1=x, y1=y, x2=x4, y2=y4, color=scaffold},
})
return result
end
function car.draw()
local pts = h(0,0, N,0, 0,N, depth)
color(0,0,1)
love.graphics.setLineWidth(5)
for i=2,#pts do
line(ox+pts[i-1].x, oy+pts[i-1].y, ox+pts[i].x, oy+pts[i].y)
end
for _, pt in ipairs(pts) do
if pt.draw then
for _,shape in ipairs(pt.draw) do
color(shape.color.r, shape.color.g, shape.color.b, shape.color.a)
if shape.type == 'circle' then
love.graphics.setLineWidth(1)
circle(shape.drawmode, ox+shape.x, oy+shape.y, shape.radius)
elseif shape.type == 'line' then
love.graphics.setLineWidth(2)
line(ox+shape.x1, oy+shape.y1, ox+shape.x2, oy+shape.y2)
end end end end end
function array_join(...)
local result = {}
for i, arg in ipairs{...} do
for _,x in ipairs(arg) do
table.insert(result, x)
end end
return result
end
No, that's pretty but too messy. The computation is partitioned but the image is full of overlapping points and lines (in spite of my efforts at using filled and hollow circles to show two things in one place). How can we reveal the overlaps? Maybe some animation?
code
local ox,oy = 300,100 -- where to start drawing local N = 800 -- size of the drawing local depth = 4 -- levels of recursion; 0 = single point local d = 0 -- instantaneous offset of the corner of the scaffold local dmax = 10 local ddd = 10 -- how fast the corner of the scaffold moves local dd = ddd -- instantaneous speed of the corner of the scaffold -- colors local primary = {r=1, g=0.8, b=0} local control = {r=0, g=0.8, b=0.8} local c = 0.8 local scaffold = {r=c, g=c, b=c} function h(x, y, xi, yi, xj, yj, n, N) if N == nil then N = n end local x3, y3 = x+xi, y+yi local x4, y4 = x+xj, y+yj if n <= 0 then local resultx, resulty = x+xi/2+yi/2, y+yi/2+yj/2 local debug = { {type='circle', drawmode='fill', x=x, y=y, radius=5, color=primary}, {type='line', x1=resultx, y1=resulty, x2=x, y2=y, color=primary}, {type='circle', drawmode='line', x=x3, y=y3, radius=10, color=control}, {type='line', x1=resultx, y1=resulty, x2=x3, y2=y3, color=control}, {type='circle', drawmode='line', x=x4, y=y4, radius=10, color=control}, {type='line', x1=resultx, y1=resulty, x2=x4, y2=y4, color=control}, } return {{x = resultx, y = resulty, draw=debug}} end local result = array_join( h(x, y, xj/2, yj/2, xi/2, yi/2, n-1, N), h(x+xi/2, y+yi/2, xi/2, yi/2, xj/2, yj/2, n-1, N), h(x+xi/2+xj/2, y+yi/2+yj/2, xi/2, yi/2, xj/2, yj/2, n-1, N), h(x+xi/2+xj, y+yi/2+yj, -xj/2, -yj/2, -xi/2, -yi/2, n-1, N)) -- i's and j's always share the same sign -- at least one of xi and yi is always non-zero local dir = (xi == 0) and sign(yi) or sign(xi) local xs, ys = x+(N-n)*d*dir, y+(N-n)*d*dir result[1].draw = array_join(result[1].draw, { {type='line', x1=xs, y1=ys, x2=x3, y2=y3, color=scaffold}, {type='line', x1=xs, y1=ys, x2=x4, y2=y4, color=scaffold}, }) return result end function car.draw() local pts = h(0,0, N,0, 0,N, depth) color(0,0,1) love.graphics.setLineWidth(5) for i=2,#pts do line(ox+pts[i-1].x, oy+pts[i-1].y, ox+pts[i].x, oy+pts[i].y) end for _, pt in ipairs(pts) do if pt.draw then for _,shape in ipairs(pt.draw) do color(shape.color.r, shape.color.g, shape.color.b, shape.color.a) if shape.type == 'circle' then love.graphics.setLineWidth(1) circle(shape.drawmode, ox+shape.x, oy+shape.y, shape.radius) elseif shape.type == 'line' then love.graphics.setLineWidth(2) line(ox+shape.x1, oy+shape.y1, ox+shape.x2, oy+shape.y2) end end end end end function car.update(dt) d = d+dd*dt if d >= dmax then d, dd = dmax, -ddd elseif d < 0 then d, dd = 0, ddd end end function array_join(...) local result = {} for i, arg in ipairs{...} do for _,x in ipairs(arg) do table.insert(result, x) end end return result end function sign(a) if a > 0 then return 1 elseif a < 0 then return -1 else return 0 end end
Again, pretty. But too busy; I'm not sure I'm learning anything by staring at it.
At this point I'm starting to feel overwhelmed by the number of different versions of this program I've created. They're also competing for space with just the clean Hilbert curve, and I find myself commenting and uncommenting code to bounce between the curve and its internals. I realize I can create a dedicated space for debug UIs while also extracting a few common patterns of debug UIs that might be useful to other programs.
The dedicated space can be a goofy little window manager. But Carousel has its own eponymous metaphor for giving programs their own dedicated space/screen that you can navigate using buttons along the left and right margins even on the small screen of a phone. Let's give each debug UI its own screen. Programs write data for a specific UI under a special key in a table called `Windows`, and now debug UIs in other screens can render what they find there.
Some patterns start to come into focus:
- Text log. This is trivial and doesn't require its own screen. It's the starting point for generalization. I reached for it in v2 above.
- Replay-log. The program appends groups of shapes to a log, and they appear over time in the same order they were appended to the log. In effect, we're showing time as time, just offset, a recording with adjustable speed. This is akin to v3 above.
code (150 lines)
-- Debug window with a pannable, zoomable, infinite 2D surface that plays groups of vector commands -- in a loop. -- Groups cumulate; frame 2 draws shapes from groups 1 and 2, and so on. run_screen('ticks') run_screen('widgets') function debug_window_replay_log(window_name, speeds) local I = {} if Windows == nil then Windows = {} end if Windows.__viewport == nil then Windows.__viewport = {} end if Windows[window_name] == nil then Windows[window_name] = {} end -- Windows.__viewport[window_name] = nil -- uncomment to reset viewport if Windows.__viewport[window_name] == nil then run_screen('infinite-viewport') Windows.__viewport[window_name] = run_screen_return run_screen_return = nil end local v = Windows.__viewport[window_name] local frame_index = 0 local speed_index = 1 for i,speed in ipairs(speeds) do if speed == 1 then speed_index = i end end function car.draw() local title = ('%d/%d'):format(frame_index, #Windows[window_name]) love.graphics.print(title, 100, Menu_bottom + 15) I.draw_axes() assert(frame_index < #Windows[window_name]+1) for i=1,frame_index do local shape_batch = Windows[window_name][i] I.draw_shapes(shape_batch) end -- stuff in viewport coordinates love.graphics.setColor(0.5,0.5,0.5) love.graphics.print('replay speed (shapes/s)', 50, 250-9*20) widgets.__draw() I.draw_hud() end function I.draw_shapes(batch) for i,shape in ipairs(batch) do I.draw_shape(shape) end end function I.draw_shape(shape) color(shape.r or 0.5, shape.g or 0.5, shape.b or 0.5, shape.a or 1) if shape.type == 'point' then circle('fill', v.vx(shape.x), v.vy(shape.y), 2) elseif shape.type == 'line' then line(v.vx(shape.x1), v.vy(shape.y1), v.vx(shape.x2), v.vy(shape.y2)) elseif shape.type == 'rectangle' then rect(shape.drawmode or 'fill', v.vx(shape.x), v.vy(shape.y), v.scale(shape.w), v.scale(shape.h)) elseif shape.type == 'circle' then circle(shape.drawmode or 'fill', v.vx(shape.x), v.vy(shape.y), v.scale(shape.radius)) elseif shape.type == 'text' then g.print(shape.data, v.vx(shape.x), v.vy(shape.y)) elseif shape.type == 'group' then I.draw_shapes(shape) end end function I.speed_indicator(index) local drawmode, x,y, w,h local function refresh() drawmode = 'line' x, w,h = 80, 10, 20 if speed_index >= index then drawmode = 'fill' x, w = x-1, w+2 -- make 'fill' same width as 'line' end y = Menu_bottom + 100 + #speeds*h - index*h end refresh() local draw = function() refresh() love.graphics.setColor(1,0,1) love.graphics.rectangle(drawmode, x,y, w, h) love.graphics.line(x+w, y, x+w+5, y) love.graphics.setColor(0.5,0.5,0.5) love.graphics.print(speeds[index], x+w+10, y-10) end local ispress = function(x2,y2) return x <= x2 and x2 <= x+w and y <= y2 and y2 <= y+h end local press = function() speed_index = index return true end return {draw=draw, ispress=ispress, press=press} end for i=1,#speeds do widgets['speed_indicator_'..i] = I.speed_indicator(i) end function car.update(dt) widgets.__update(dt) frame_index = frame_index + dt*speeds[speed_index] if frame_index >= #Windows[window_name] + 1 then frame_index = 0 elseif frame_index < 0 then frame_index = #Windows[window_name] end end function I.draw_axes() color(0.5,0.5,0.5) line(0, v.vy(0), Safe_width, v.vy(0)) line(v.vx(0), 0, v.vx(0), Safe_height) if ticks == nil then return end local xlo, xhi = ticks(v.sx(0), v.sx(Safe_width)) for i=0,10 do local x = xlo+i/10*(xhi-xlo) local vx, vy = v.vx(x), v.vy(0) line(vx, vy, vx, vy+5) g.print(x, vx-10, vy+10) end local ylo, yhi = ticks(v.sy(Menu_bottom), v.sy(Safe_height)) for i=0,10 do local y = ylo+i/10*(yhi-ylo) local vx, vy = v.vx(0), v.vy(y) line(vx, vy, vx+5, vy) g.print(y, vx+10, vy+5) end end function I.draw_hud() color(0.5, 0.5, 0.5) for _,id in ipairs(touches()) do local x, y = touch(id) circle('fill', x, y, 10) end end car.mouse_press = v.mouse_press car.mouse_move = v.mouse_move car.mouse_release = v.mouse_release car.mouse_wheel_move = v.mouse_wheel_move function car.touch_press(id, x,y, ...) if widgets.__press(x,y, id) then return end v.touch_press(id, x,y, ...) end car.touch_move = v.touch_move function car.touch_release(id, x,y, ...) if widgets.__release(x,y, id) then return end v.touch_release(id, x,y, ...) end end -- function debug_window_replay debug_window_replay_log('replay', {-10, -4, -2, -1, -0.5, -0.25, -0.1, 0, 0.1, 0.25, 0.5, 1, 2, 4, 10})
- Draw shapes on a surface without any further structure, and always draw them all. v4 and v5 demonstrated this, but we can also support panning and zooming on the surface with multitouch support.
code (85 lines)
-- Debug window with a pannable, zoomable, infinite 2D surface, that plots vector commands run_screen('ticks') function debug_window_surface(window_name) local I = {} if Windows == nil then Windows = {} end if Windows.__viewport == nil then Windows.__viewport = {} end if Windows[window_name] == nil then Windows[window_name] = {} end -- Windows.__viewport[window_name] = nil -- uncomment to reset viewport if Windows.__viewport[window_name] == nil then run_screen('infinite-viewport') Windows.__viewport[window_name] = run_screen_return run_screen_return = nil end local v = Windows.__viewport[window_name] function car.draw() I.draw_axes() for _,shape in ipairs(Windows[window_name]) do I.draw_shape(shape) end I.draw_hud() end function I.draw_shape(shape) color(shape.r or 0.5, shape.g or 0.5, shape.b or 0.5, shape.a or 1) if shape.type == 'point' then circle('fill', v.vx(shape.x), v.vy(shape.y), 2) elseif shape.type == 'line' then line(v.vx(shape.x1), v.vy(shape.y1), v.vx(shape.x2), v.vy(shape.y2)) elseif shape.type == 'rectangle' then rect(shape.drawmode or 'fill', v.vx(shape.x), v.vy(shape.y), v.scale(shape.w), v.scale(shape.h)) elseif shape.type == 'circle' then circle(shape.drawmode or 'fill', v.vx(shape.x), v.vy(shape.y), v.scale(shape.radius)) elseif shape.type == 'text' then g.print(shape.data, v.vx(shape.x), v.vy(shape.y)) elseif shape.type == 'group' then I.draw_shapes(shape) end end function I.draw_axes() color(0.5,0.5,0.5) line(0, v.vy(0), Safe_width, v.vy(0)) line(v.vx(0), 0, v.vx(0), Safe_height) if ticks == nil then return end local xlo, xhi = ticks(v.sx(0), v.sx(Safe_width)) for i=0,10 do local x = xlo+i/10*(xhi-xlo) local vx, vy = v.vx(x), v.vy(0) line(vx, vy, vx, vy+5) g.print(x, vx-10, vy+10) end local ylo, yhi = ticks(v.sy(Menu_bottom), v.sy(Safe_height)) for i=0,10 do local y = ylo+i/10*(yhi-ylo) local vx, vy = v.vx(0), v.vy(y) line(vx, vy, vx+5, vy) g.print(y, vx+10, vy+5) end end function I.draw_hud() color(0.5, 0.5, 0.5) for _,id in ipairs(touches()) do local x, y = touch(id) circle('fill', x, y, 10) end end car.mouse_press = v.mouse_press car.mouse_move = v.mouse_move car.mouse_release = v.mouse_release car.mouse_wheel_move = v.mouse_wheel_move car.touch_press = v.touch_press car.touch_move = v.touch_move car.touch_release = v.touch_release end -- function debug_window_surface debug_window_surface('surface')
- A graphical log. Show time on the y-axis. It didn't help much here, but you can see it in action on a different program.
code (80 lines)
-- Debug window with a bounded pannable, zoomable 2D surface that contains a sequence of drawings -- down the y axis. Like a text log, but graphical. -- ox and oy describe the coordinates from which to start drawing each image. w,h describe the size to -- draw. -- All 4 arguments are in the coordinates of the drawing. function debug_window_plot_log(window_name, ox,oy, w,h) local I = {} if Windows == nil then Windows = {} end if Windows.__viewport == nil then Windows.__viewport = {} end if Windows[window_name] == nil then Windows[window_name] = {} end -- Windows.__viewport[window_name] = nil -- uncomment to reset viewport and force load screen if Windows.__viewport[window_name] == nil then run_screen('infinite-viewport') Windows.__viewport[window_name] = run_screen_return run_screen_return = nil end local v = Windows.__viewport[window_name] function car.draw() local x0,y0 = 0,0 for _,batch in ipairs(Windows[window_name]) do I.draw_shapes(batch, x0,y0) y0 = y0 + h + 50 end I.draw_hud() end function I.draw_shapes(batch, x0,y0) color(0.5,0.5,0.5) line(v.vx(x0), v.vy(y0-oy), v.vx(x0+w), v.vy(y0-oy)) line(v.vx(x0-ox), v.vy(y0+0), v.vx(x0-ox), v.vy(y0+h)) for _,shape in ipairs(batch) do I.draw_shape(shape, x0-ox,y0-oy) end end function I.draw_shape(shape, x0,y0) color(shape.r or 0.5, shape.g or 0.5, shape.b or 0.5, shape.a or 1) if shape.type == 'point' then circle('fill', v.vx(x0+shape.x), v.vy(y0+shape.y), 2) elseif shape.type == 'line' then line(v.vx(x0+shape.x1), v.vy(y0+shape.y1), v.vx(x0+shape.x2), v.vy(y0+shape.y2)) elseif shape.type == 'rectangle' then rect(shape.drawmode or 'fill', v.vx(x0+shape.x), v.vy(y0+shape.y), v.scale(shape.w), v.scale(shape.h)) elseif shape.type == 'circle' then circle(shape.drawmode or 'fill', v.vx(x0+shape.x), v.vy(y0+shape.y), v.scale(shape.radius)) elseif shape.type == 'text' then g.print(shape.data, v.vx(x0+shape.x), v.vy(y0+shape.y)) elseif shape.type == 'group' then I.draw_shapes(shape, x0,y0) end end function I.draw_hud() color(0.5, 0.5, 0.5) for _,id in ipairs(touches()) do local x, y = touch(id) circle('fill', x, y, 10) end end function car.keychord_press(chord) if chord == 'down' then v.v.y = v.v.y + h + 50 elseif chord == 'up' then if v.v.y > 0 then v.v.y = v.v.y - h - 50 end end end car.mouse_press = v.mouse_press car.mouse_move = v.mouse_move car.mouse_release = v.mouse_release car.mouse_wheel_move = v.mouse_wheel_move car.touch_press = v.touch_press car.touch_move = v.touch_move car.touch_release = v.touch_release end -- function debug_window_plot_log debug_window_plot_log('log', 0, 0, 500,500)
- Exploding view drawings give me a way to overlay and decompose sub-computations.
code (200 lines)
-- Debug window with a bounded pannable, zoomable 2D surface that contains a sequence of drawings -- with nested structure -- Drawings can have type line, circle, etc. and also group. function debug_window_explode(window_name, w,h) local I = {} if Windows == nil then Windows = {} end if Windows.__viewport == nil then Windows.__viewport = {} end if Windows[window_name] == nil then Windows[window_name] = {} end -- Windows.__viewport[window_name] = nil -- uncomment to reset viewport if Windows.__viewport[window_name] == nil then -- origin at center run_screen('infinite-viewport') Windows.__viewport[window_name] = run_screen_return run_screen_return = nil local v = Windows.__viewport[window_name] v.x, v.y = -5, -5*Safe_height/Safe_width v.w, v.h = -2*v.x, -2*v.y v.zoom = Safe_width/v.w end local v = Windows.__viewport[window_name] ---- lay out the state of the log local layout = {} -- a flat list of (sub)charts to draw local pad = 500 -- return some options for places to put r near r2 -- ignores r.x/r.y, cares only about r.w/r.h function I.adjacent_options(r, r2) return { {x=r2.x - r.w - pad, y=r2.y, w=r.w, h=r.h}, -- left {x=r2.x+r2.w+pad, y=r2.y, w=r.w, h=r.h}, -- right {x=r2.x, y=r2.y - r.h - pad, w=r.w, h=r.h}, -- above {x=r2.x, y=r2.y+r2.h+pad, w=r.w, h=r.h}, -- right } end -- where should we move r to avoid overlap with multiple rs? function I.place(r, rs) for i, r2 in ipairs(rs) do local options = I.adjacent_options(r, r2) for _, r1 in ipairs(options) do if not I.aabb_any(r1, rs) then return r1 end end end return r end function I.aabb_any(r, rs) for _, r2 in ipairs(rs) do if I.aabb(r, r2) then return true end end end function I.aabb(r1, r2) return r1.x < r2.x+r2.w+pad and r1.x+r1.w+pad > r2.x and r1.y < r2.y+r2.h+pad and r1.y+r1.h+pad > r2.y end -- alternative approach: biased to place near some candidates (a subset of rs) -- will give up if cands are surrounded completely function I.place_near(r, cands, rs) for i, r2 in ipairs(cands) do local options = I.adjacent_options(r, r2) for j, r1 in ipairs(options) do if not I.aabb_any(r1, rs) then return r1 end end end assert(false) end -- a batch is a group and all its descendants function I.place_batch(batch) batch.w, batch.h = w, h local pos = I.place(batch, layout) pos.data = batch table.insert(layout, pos) end function I.place_batch_near(batch, cands) batch.w, batch.h = w, h local pos = I.place_near(batch, cands, layout) pos.data = batch table.insert(layout, pos) return pos end function I.place_lower_batches(batch) for _, b in ipairs(batch) do if #b > 0 then I.place_batch(b) end end for _, b in ipairs(batch) do if b.type == 'group' then I.place_lower_batches(b) end end end function I.title(msg) return {type='text', data=msg, x=50, y=-10000} end function I.handle_layout_touch(x,y) local sx,sy = v.sx(x), v.sy(y) for i,batch in ipairs(layout) do if I.within_rect(batch, sx,sy) then if batch.expanded then return end batch.expanded = true local cands = {batch} for j, b in ipairs(batch.data) do if b.type == 'group' and #b > 0 then local pos = I.place_batch_near(b, cands) table.insert(cands, pos) end end return true end end end function I.within_rect(rect, x,y) return rect.x <= x and x <= rect.x+rect.w and rect.y <= y and y <= rect.y+rect.h end function I.collapse_all(batch) batch.expanded = nil for _, b in ipairs(batch) do if b.type == 'group' then I.collapse_all(b) end end end -- assume window has a single object for now local save_data -- remember data so we redraw if it changes function car.update(dt) if #Windows[window_name] == 0 then return end if save_data == Windows[window_name][1] then return end layout = {} save_data = Windows[window_name][1] save_data.x, save_data.y = 0, 0 I.collapse_all(save_data) -- we shove some data hackily in window data, clear that out I.place_batch(save_data) -- I.place_lower_batches(save_data) -- uncomment this to expand all end -- draw batches according to the layout function car.draw() for _, batch in ipairs(layout) do I.draw_batch(batch.data, batch.x, batch.y) end I.draw_hud() end function I.draw_batch(batch, x0,y0) color(0.5,0.5,0.5) line(v.vx(x0), v.vy(y0+0), v.vx(x0+w), v.vy(y0+0)) line(v.vx(x0+0), v.vy(y0), v.vx(x0+0), v.vy(y0+h)) I.draw_shapes(batch, x0,y0, true) end function I.draw_shapes(batch, x0,y0, top) for _,shape in ipairs(batch) do if top or not shape.at_top then I.draw_shape(shape, x0,y0) end end end function I.draw_shape(shape, x0,y0) color(shape.r or 0.5, shape.g or 0.5, shape.b or 0.5, shape.a or 1) if shape.type == 'point' then circle('fill', v.vx(x0+shape.x), v.vy(y0+shape.y), 2) elseif shape.type == 'line' then if shape.name then print(shape.name) end line(v.vx(x0+shape.x1), v.vy(y0+shape.y1), v.vx(x0+shape.x2), v.vy(y0+shape.y2)) elseif shape.type == 'rectangle' then rect(shape.drawmode or 'fill', v.vx(x0+shape.x), v.vy(y0+shape.y), v.scale(shape.w), v.scale(shape.h)) elseif shape.type == 'circle' then circle(shape.drawmode or 'fill', v.vx(x0+shape.x), v.vy(y0+shape.y), v.scale(shape.radius)) elseif shape.type == 'text' then g.print(shape.data, v.vx(x0+shape.x), v.vy(y0+shape.y)) elseif shape.type == 'group' then I.draw_shapes(shape, x0,y0) end end function I.draw_hud() color(0.5, 0.5, 0.5) for _,id in ipairs(touches()) do local x, y = touch(id) circle('fill', x, y, 10) end end car.mouse_press = v.mouse_press car.mouse_move = v.mouse_move car.mouse_release = v.mouse_release car.mouse_wheel_move = v.mouse_wheel_move function car.touch_press(id, x,y, ...) if I.handle_layout_touch(x,y) then return end v.touch_press(id, x,y, ...) end car.touch_move = v.touch_move car.touch_release = v.touch_release end -- function debug_window_explode debug_window_explode('nested', 500,500)
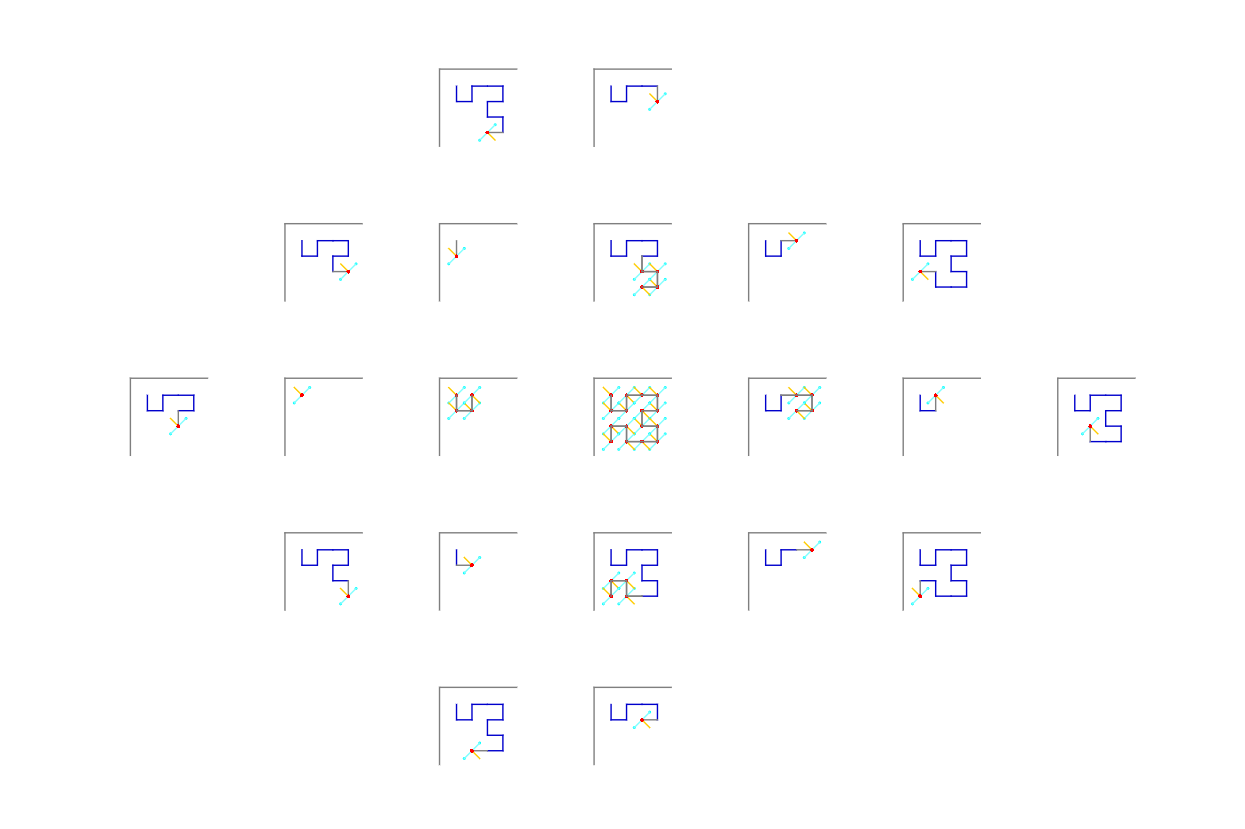
Generating data for the exploding view
function h(x, y, xi, yi, xj, yj, n, log, points_so_far) log.type = 'group' local p = points_so_far if #p > 0 then for i=2,#p do table.insert(log, {type='line', x1=p[i-1].x, y1=p[i-1].y, x2=p[i].x, y2=p[i].y, r=0, g=0, b=0.8, at_top = true, }) end end if n <= 0 then local resultx, resulty = x+xi/2+yi/2, y+yi/2+yj/2 if p and #p > 0 then table.insert(log, {type='line', x1=p[#p].x, y1=p[#p].y, x2=resultx, y2=resulty, r=0.5, g=0.5, b=0.5, }) end local x3, y3 = x+xi, y+yi local x4, y4 = x+xj, y+yj insert_all(log, {type='circle', drawmode='fill', x=x, y=y, radius=2, r=1,g=0.8,b=0}, {type='line', x1=resultx, y1=resulty, x2=x, y2=y, r=1,g=0.8,b=0}, {type='circle', drawmode='line', x=x3, y=y3, radius=5, r=0, g=1, b=1}, {type='line', x1=resultx, y1=resulty, x2=x3, y2=y3, r=0.5,g=1,b=1}, {type='circle', drawmode='line', x=x4, y=y4, radius=5, r=0, g=1, b=1}, {type='line', x1=resultx, y1=resulty, x2=x4, y2=y4, r=0.5,g=1,b=1}, {type='point', x=resultx, y=resulty,r=1,g=0,b=0} ) return {{x = resultx, y = resulty, draw=debug}} end local points_so_far_at_start = points_so_far local log1, log2, log3, log4 = {}, {}, {}, {} local res1 = h(x, y, xj/2, yj/2, xi/2, yi/2, n-1, log1, points_so_far) points_so_far = array_join(points_so_far, res1) local res2 = h(x+xi/2, y+yi/2, xi/2, yi/2, xj/2, yj/2, n-1, log2, points_so_far) points_so_far = array_join(points_so_far, res2) local res3 = h(x+xi/2+xj/2, y+yi/2+yj/2, xi/2, yi/2, xj/2, yj/2, n-1, log3, points_so_far) points_so_far = array_join(points_so_far, res3) local res4 = h(x+xi/2+xj, y+yi/2+yj, -xj/2, -yj/2, -xi/2, -yi/2, n-1, log4, points_so_far) insert_all(log, log1, log2, log3, log4) local result = array_join(res1, res2, res3, res4) if #points_so_far_at_start > 0 then local p = points_so_far_at_start table.insert(log, {type='line', x1=p[#p].x, y1=p[#p].y, x2=result[1].x, y2=result[1].y, r=0.5, g=0.5, b=0.5, at_top=true, }) end local p = result for i=2,#p do table.insert(log, {type='line', x1=p[i-1].x, y1=p[i-1].y, x2=p[i].x, y2=p[i].y, r=0.5, g=0.5, b=0.5, at_top=true, }) end append(points_so_far, result) return result end function insert_all(h, ...) local args = {...} for _, arg in ipairs(args) do table.insert(h, arg) end end -- mutate r1 function append(r, r1) for _,x in ipairs(r1) do table.insert(r, x) end end function array_join(...) local result = {} for i, arg in ipairs{...} do for _,x in ipairs(arg) do table.insert(result, x) end end return result end function dbg(window_name, data) table.insert(Windows[window_name], data) end if Windows == nil then Windows = {} end Windows.surface = {} Windows.log = {} local log = {} local pts = h(60, 60, 400, 0, 0, 400, 2, log, {}) Windows.nested = {log} local ox,oy = 200,200 function car.draw() color(0,0,0) for i=2,#pts do line(ox+pts[i-1].x, oy+pts[i-1].y, ox+pts[i].x, oy+pts[i].y) end end
They require a little more thought to use. Every call creates a group of shapes, and the groups created by recursive calls become children of their caller. Groups can thus contain more groups, to arbitrary depth. A group draws everything under it when collapsed, and expanding a group corresponds to giving its child groups their own disjoint space on the surface.
- Replay. After working through these options I think of another pattern. What I need is to be able to animate things, but in a different order than I computed them. Made-up time. Show higher levels together, pretend the computation was breadth-first.
code (150 lines)
-- Debug window with a pannable, zoomable, infinite 2D surface that plays groups of vector commands -- in a loop. run_screen('ticks') run_screen('widgets') function debug_window_replay(window_name, speeds) local I = {} if Windows == nil then Windows = {} end if Windows.__viewport == nil then Windows.__viewport = {} end if Windows[window_name] == nil then Windows[window_name] = {} end -- Windows.__viewport[window_name] = nil -- uncomment to reset viewport if Windows.__viewport[window_name] == nil then run_screen('infinite-viewport') Windows.__viewport[window_name] = run_screen_return run_screen_return = nil end local v = Windows.__viewport[window_name] local frame_index = 0 local speed_index = 1 for i,speed in ipairs(speeds) do if speed == 1 then speed_index = i end end function car.draw() local title = ('%d/%d'):format(frame_index, #Windows[window_name]) love.graphics.print(title, 100, Menu_bottom + 15) I.draw_axes() local f = floor(frame_index) assert(f <= #Windows[window_name]) I.draw_shapes(Windows[window_name][f]) -- stuff in viewport coordinates love.graphics.setColor(0.5,0.5,0.5) love.graphics.print('replay speed (shapes/s)', 50, 250-9*20) widgets.__draw() I.draw_hud() end function I.draw_shapes(batch) if batch == nil then return end for i,shape in ipairs(batch) do I.draw_shape(shape) end end function I.draw_shape(shape) color(shape.r or 0.5, shape.g or 0.5, shape.b or 0.5, shape.a or 1) if shape.type == 'point' then circle('fill', v.vx(shape.x), v.vy(shape.y), 2) elseif shape.type == 'line' then line(v.vx(shape.x1), v.vy(shape.y1), v.vx(shape.x2), v.vy(shape.y2)) elseif shape.type == 'rectangle' then rect(shape.drawmode or 'fill', v.vx(shape.x), v.vy(shape.y), v.scale(shape.w), v.scale(shape.h)) elseif shape.type == 'circle' then circle(shape.drawmode or 'fill', v.vx(shape.x), v.vy(shape.y), v.scale(shape.radius)) elseif shape.type == 'text' then g.print(shape.data, v.vx(shape.x), v.vy(shape.y)) elseif shape.type == 'group' then I.draw_shapes(shape) end end function I.speed_indicator(index) local drawmode, x,y, w,h local function refresh() drawmode = 'line' x, w,h = 80, 10, 20 if speed_index >= index then drawmode = 'fill' x, w = x-1, w+2 -- make 'fill' same width as 'line' end y = Menu_bottom + 100 + #speeds*h - index*h end refresh() local draw = function() refresh() love.graphics.setColor(1,0,1) love.graphics.rectangle(drawmode, x,y, w, h) love.graphics.line(x+w, y, x+w+5, y) love.graphics.setColor(0.5,0.5,0.5) love.graphics.print(speeds[index], x+w+10, y-10) end local ispress = function(x2,y2) return x <= x2 and x2 <= x+w and y <= y2 and y2 <= y+h end local press = function() speed_index = index return true end return {draw=draw, ispress=ispress, press=press} end for i=1,#speeds do widgets['speed_indicator_'..i] = I.speed_indicator(i) end function car.update(dt) widgets.__update(dt) frame_index = frame_index + dt*speeds[speed_index] if frame_index >= #Windows[window_name] + 1 then frame_index = 0 elseif frame_index < 0 then frame_index = #Windows[window_name] end end function I.draw_axes() color(0.5,0.5,0.5) line(0, v.vy(0), Safe_width, v.vy(0)) line(v.vx(0), 0, v.vx(0), Safe_height) if ticks == nil then return end local xlo, xhi = ticks(v.sx(0), v.sx(Safe_width)) for i=0,10 do local x = xlo+i/10*(xhi-xlo) local vx, vy = v.vx(x), v.vy(0) line(vx, vy, vx, vy+5) g.print(x, vx-10, vy+10) end local ylo, yhi = ticks(v.sy(Menu_bottom), v.sy(Safe_height)) for i=0,10 do local y = ylo+i/10*(yhi-ylo) local vx, vy = v.vx(0), v.vy(y) line(vx, vy, vx+5, vy) g.print(y, vx+10, vy+5) end end function I.draw_hud() color(0.5, 0.5, 0.5) for _,id in ipairs(touches()) do local x, y = touch(id) circle('fill', x, y, 10) end end car.mouse_press = v.mouse_press car.mouse_move = v.mouse_move car.mouse_release = v.mouse_release car.mouse_wheel_move = v.mouse_wheel_move function car.touch_press(id, x,y, ...) if widgets.__press(x,y, id) then return end v.touch_press(id, x,y, ...) end car.touch_move = v.touch_move function car.touch_release(id, x,y, ...) if widgets.__release(x,y, id) then return end v.touch_release(id, x,y, ...) end end -- function debug_window_replay debug_window_replay('replay', {-10, -4, -2, -1, -0.5, -0.25, -0.1, 0, 0.1, 0.25, 0.5, 1, 2, 4, 10})
Visualize all calls at the same depth in the same frame of the replay animation.
if then Windows = {} end if == nil then Windows.replay = {} end function h(x, y, xi, yi, xj, yj, n, depth) if depth == nil then depth = 1 end if Windows.replay[depth] == nil then Windows.replay[depth] = {type='group'} end local r = 5 table.insert(Windows.replay[depth], {type='group', {type='circle', drawmode='fill', x=x, y=y, radius=r}, {type='circle', drawmode='line', x=x+xi, y=y+yi, radius=r}, {type='circle', drawmode='line', x=x+xj, y=y+yj, radius=r}, {type='line', x1=x, y1=y, x2=x+xi, y2=y+yi}, {type='line', x1=x, y1=y, x2=x+xj, y2=y+yj}, }) if n <= 0 then return {x+xi/2+xj/2, y+yi/2+yj/2} end return array_join( h(x, y, xj/2, yj/2, xi/2, yi/2, n-1, depth+1), h(x+xi/2, y+yi/2, xi/2, yi/2, xj/2, yj/2, n-1, depth+1), h(x+xi/2+xj/2, y+yi/2+yj/2, xi/2, yi/2, xj/2, yj/2, n-1, depth+1), h(x+xi/2+xj, y+yi/2+yj, -xj/2, -yj/2, -xi/2, -yi/2, n-1, depth+1)) end function array_join(...) local result = {} for i, arg in ipairs{...} do for _,x in ipairs(arg) do table.insert(result, x) end end return result end if Windows == nil then Windows = {} end Windows.replay = {} local pts = h(60, 60, 800, 0, 0, 800, --[[n]] 2) function car.draw() color(0,0,0) line(unpack(pts)) endAdd some color and offset the lines to separate them visually:
the minor code changes made
if Windows == nil then Windows = {} end if Windows.replay == nil then Windows.replay = {} end function h(x, y, xi, yi, xj, yj, n, depth) if depth == nil then depth = 1 end if Windows.replay[depth] == nil then Windows.replay[depth] = {type='group'} end local r = 5 local x1,y1, x2,y2, x3,y3 x1 = x+xi/10+xj/10 y1 = y+yi/10+yj/10 if xi == 0 then x2 = x + xj/10 y2 = y + yi*9/10 else x2 = x + xi*9/10 y2 = y + yj/10 end if xj == 0 then x3 = x + xi/10 y3 = y + yj*9/10 else x3 = x + xj*9/10 y3 = y + yi/10 end table.insert(Windows.replay[depth], {type='group', {type='circle', drawmode='fill', x=x1, y=y1, radius=r, r=1,g=0.8,b=0}, {type='line', x1=x1, y1=y1, x2=x2, y2=y2, r=0, g=1, b=1}, {type='line', x1=x1, y1=y1, x2=x3, y2=y3, r=1, g=0, b=1}, }) if n <= 0 then return {x+xi/2+xj/2, y+yi/2+yj/2} end return array_join( h(x, y, xj/2, yj/2, xi/2, yi/2, n-1, depth+1), h(x+xi/2, y+yi/2, xi/2, yi/2, xj/2, yj/2, n-1, depth+1), h(x+xi/2+xj/2, y+yi/2+yj/2, xi/2, yi/2, xj/2, yj/2, n-1, depth+1), h(x+xi/2+xj, y+yi/2+yj, -xj/2, -yj/2, -xi/2, -yi/2, n-1, depth+1)) end function array_join(...) local result = {} for i, arg in ipairs{...} do for _,x in ipairs(arg) do table.insert(result, x) end end return result end if Windows == nil then Windows = {} end Windows.replay = {} local pts = h(60, 60, 800, 0, 0, 800, --[[n]] 2) function car.draw() color(0,0,0) line(unpack(pts)) end
I stare at this last one a while.
A small insight arrives. To draw a hilbert curve you need only to answer this question:
Given a square divided into 4 quadrants, in what order should the quadrants be visited to efficiently fill the space?An answer to this question gives you the Hilbert curve as you subdivide quadrants. Given a sequence of quadrants at the finest level, the Hilbert curve simply connects up their centroids.
And the image above gives the answer to this question. The magenta line (bearing: xj,yj) shows for each square the quadrants where the start and end point lie. And the cyan line (bearing: xi,yi) indicates the direction of the remaining 2 quadrants, the direction the curve must head out to before returning to the magenta line.
The job of a debug UI is done when it forms a picture in my mind. However, for a blog post I'll clearly draw out the picture in my mind:
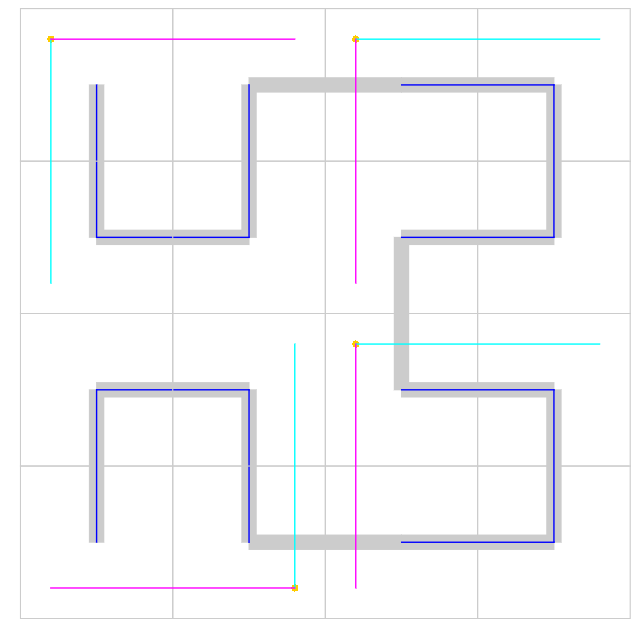
The Hilbert curve always starts at the (center of the) quadrant containing the corner of the magenta and cyan lines (quadrant x,y), continues along the cyan direction (bearing xi,yi) and then turns in the magenta direction (bearing xj,yj) before returning to the magenta quadrants. Convince yourself this is true in the above image!
Perhaps this is obvious to you. Perhaps it was hard for me to get to because I was thinking in terms of lines, conditioned by my starting point with L-systems. I didn't attend enough to the quadrants.
Perhaps you're still mystified. Perhaps it just took me a while to get used to it all, and gain some illusion of understanding. Perhaps I'd have gotten there with one of the earlier visualizations, if I just stared at it a while. It's certainly true that it's been a slow, soaking understanding rather than a flash of insight. Attributing an outcome to a single cause is always a fraught exercise.
I'm going to keep using these patterns of debug UIs. Hopefully I won't encounter too many more such patterns before completing a basis set for all seasons.
fine print
Some of the debug UIs above require a couple of additional screens of code:
widgets contains a simple pattern for creating UI elements (45 lines)
-- helper screen for creating UI widgets on screen
widgets = {} -- global; clear stuff from any previous windows
-- still ugly, though; you'll see cruft when you switch screens. TODO
long_press_duration = 1
function widgets.__draw()
for name,w in pairs(widgets) do
if type(name) ~= 'string' or name:find('__') == nil and w.draw then
w.draw()
end end end
function widgets.__press(x,y, b)
for name,w in pairs(widgets) do
if type(name) ~= 'string' or name:find('__') == nil then
if w.ispress and w.ispress(x,y) and w.press then
return w.press()
end end end end
function widgets.__update(dt)
local x, y = App.mouse_x(), App.mouse_y()
local mouse_down = App.mouse_down(1)
for name,w in pairs(widgets) do
if name:find('__') == nil then
if w.update then w.update(dt, x,y) end
if w.long_press then
if mouse_down and w.ispress(x,y) then
if w.press_time == nil then
w.press_time = 0
else
w.press_time = w.press_time+dt
if w.press_time > long_press_duration then
w.long_press()
w.press_time = nil
end
end
else
w.press_time = nil
end
end end end end
function widgets.__release(x,y, b)
for name,w in pairs(widgets) do
if type(name) ~= 'string' or name:find('__') == nil then
if w.ispress and w.ispress(x,y) and w.release then
return w.release()
end end end end
ticks decides where to show ticks on the x- and y-axis based on the current viewport (40 lines)
function ticks(lo, hi)
local om = order_of_magnitude(hi-lo)
return approximate(lo, om), approximate_up(hi, om)
end
function order_of_magnitude(n)
return floor(math.log(abs(n))/math.log(10))
end
function approximate(n, zeros)
-- turn n into a number with n zeros
if zeros >= 0 then
for i=1,zeros do n = n/10 end
else
for i=zeros,0 do n = n*10 end
end
n = floor(n)
if zeros >= 0 then
for i=1,zeros do n = n*10 end
else
for i=zeros,0 do n = n/10 end
end
return n
end
function approximate_up(n, zeros)
-- turn n into a number with n zeros
if zeros >= 0 then
for i=1,zeros do n = n/10 end
else
for i=zeros,0 do n = n*10 end
end
n = ceil(n)
if n == 0 then n = 1 end
if zeros >= 0 then
for i=1,zeros do n = n*10 end
else
for i=zeros,0 do n = n/10 end
end
return n
end
infinite-viewport implements pan and zoom gestures for mouse and multitouch screen (120 lines)
-- run this screen to get an infinite viewport with mouse/touch handlers for panning/zooming
-- TODO: how to allow screens to use this while also tweaking the mouse handler for themselves?
local M = {} -- interface of methods that can be used to draw to the surface
local I = {} -- internals
-- initialize viewport with origin at center
M.v = {x=-5, y=-5*Safe_height/Safe_width}
M.v.w = -2*M.v.x
M.v.h = -2*M.v.y
M.v.zoom = Safe_width/M.v.w
local v = M.v
local f,s = nil -- ids of first and second touches
local start, curr = {}, {} -- coords of touches
local initzoom = nil
local initzoompos = nil -- for zooming using mouse wheel, in viewport coordinates
local initpos = nil -- for panning, in surface coordinates
-- handle mouse and touch the same way
function M.mouse_press(x,y, b) car.touch_press('mouse', x,y) end
M.mousepressed = M.mouse_press
function M.mouse_move(x,y) car.touch_move('mouse', x,y) end
M.mousemoved = M.mouse_move
function M.mouse_release(x,y, b) car.touch_release('mouse', x,y) end
M.mousereleased = M.mouse_release
function M.touch_press(id, x,y, ...)
if f == 'mouse' then -- redo
f, s, start.mouse, curr.mouse = nil
end
if f == nil then
f = id
initpos = {x=v.x, y=v.y}
else
s = id
initzoom = v.zoom
end
start[id] = {x=x, y=y}
curr[id] = {x=x, y=y}
end
M.touchpressed = M.touch_press
function M.touch_release(id, x,y, ...)
f,s = nil
start, curr = {}, {}
initzoom, initzoompos, initpos = nil
end
M.touchreleased = M.touch_release
function M.touch_move(id, x,y, ...)
initzoompos = nil -- assume mouse wheel never moves the mouse, mouse moving is between uses of the wheel
if start[id] then
curr[id] = {x=x, y=y}
if s then
local oldzoom = v.zoom
v.zoom = dist(curr[f], curr[s])/dist(start[f], start[s])*initzoom
I.adjust_viewport(oldzoom, v.zoom)
elseif f then
v.x = initpos.x + M.iscale(start[f].x - x)
v.y = initpos.y + M.iscale(start[f].y - y)
end end end
M.touchmoved = M.touch_move
-- on a computer use the mouse wheel to zoom and pan
function M.mouse_wheel_move(dx,dy)
local keydown = love.keyboard.isDown
if keydown('lctrl') or keydown('rctrl') then
if initzoompos == nil then
local mx,my = love.mouse.getPosition()
initzoompos = {x=mx, y=my}
end
local sx, sy = M.sx(initzoompos.x), M.sy(initzoompos.y)
v.zoom = (1+dy/10)*v.zoom
v.x = sx - M.iscale(initzoompos.x)
v.y = sy - M.iscale(initzoompos.y)
local sx2,sy2 = M.sx(initzoompos.x), M.sy(initzoompos.y)
else
v.x = v.x + v.w/10*dx
v.y = v.y - v.h/10*dy
end
end
M.wheelmoved = M.mouse_wheel_move
function I.adjust_viewport(oldzoom, zoom)
-- ensure centroid of fingers remains in view
local c = centroid(curr[f], curr[s])
v.x = v.x + c.x/oldzoom - c.x/zoom
v.y = v.y + c.y/oldzoom - c.y/zoom
end
-- the interface for dealing with the viewport
function M.vx(sx) return M.scale(sx-v.x) end
function M.vy(sy) return M.scale(sy-v.y) end
function M.scale(d) return d*v.zoom end
function M.sx(vx) return v.x + M.iscale(vx) end
function M.sy(vy) return v.y + M.iscale(vy) end
function M.iscale(d) return d/v.zoom end
-- map for heterogeneous array of x, y
function M.vxy(arr)
local result = {}
for i=1,#arr, 2 do
table.insert(result, M.vx(arr[i]))
table.insert(result, M.vy(arr[i+1]))
end
return result
end
-- some helpers
-- these feel timeless enough I'm exporting them
function centroid(a, b)
return{x=(a.x+b.x)/2, y=(a.y+b.y)/2}
end
function dist(p1, p2)
return ((p2.x-p1.x)^2 + (p2.y-p1.y)^2) ^ 0.5
end
return M
Comments gratefully appreciated. Please send them to me by any method of your choice and I'll include them here.