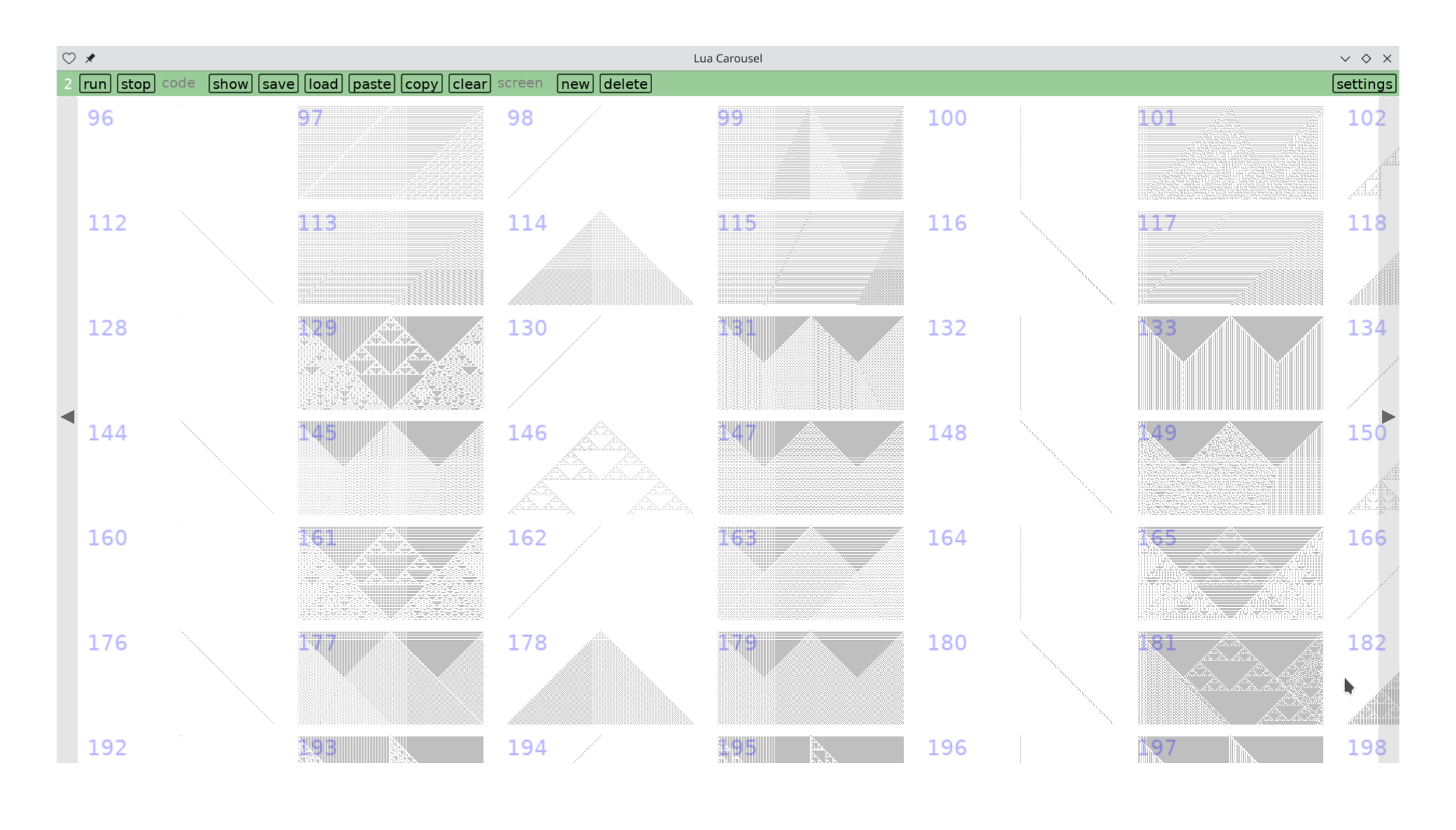
To recap, you basically have a line of cells that can be in one of two states ('alive' or 'dead') and rules that decide how a cell's state evolves based on the state of its immediate neighbors to the left and right. The images below show a snapshot of time in a row of pixels, and time advancing from the top row of pixels to the bottom.
Starting from a single live cell, of the 256 rules 16 immediately wink out (empty grids in the picture below), 16 don't change (vertical lines), 48 move the cell (24 each to the left and right), 30 grow into triangles over time (6 each to the left and right and 18 on both), 18 form Sierpinski patterns and 22 are more chaotic. Here's a detail in Lua Carousel where you can see many of these types.
However, things look different if you start from a random configuration of live and dead cells. Seemingly well-behaved rules hide subtleties, and seeming patterns vanish.
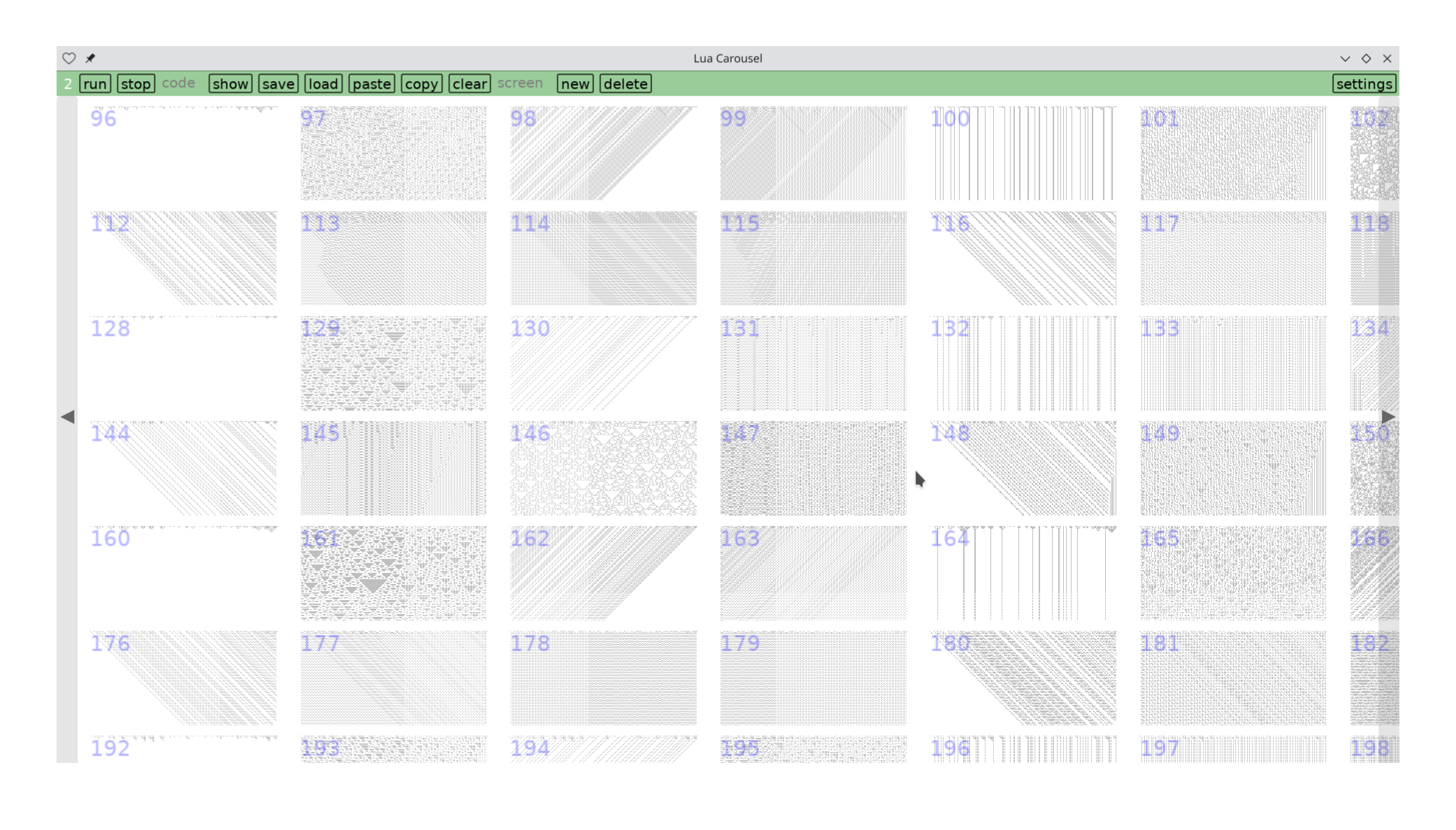
For a given rule, different random initial configurations largely look the same from a distance, which suggests random selection yields more realistic pictures for a rule.
Eye-balling the surface, I think 47/256 rules are chaotic.
Rule 30 is the famous one, but my favorites are rule 150 and 165.

(I've also been skimming Stephen Wolfram's "A New Kind of Science" as I do this. Wolfram separates "nested" from "random" patterns, but that seems to be an artifact of starting with a single live cell. "Nested" patterns (like Sierpinski triangles) are just a milder kind of chaos our visual cortex can get a grip on.)
Starting with a single live cell is 'simple' but grossly incomplete, exercising only scenarios 0, 1, 2, and 4 in the first step.
And if we truly care about simple, why not just start with all dead cells? Rules don't care.
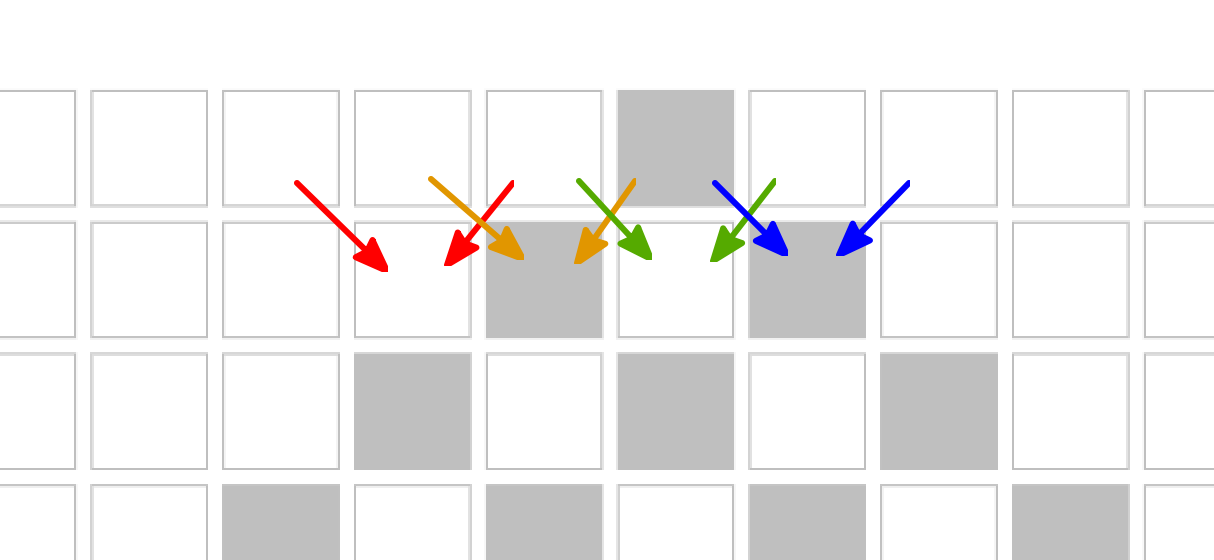
Anyways, I see two fairly simple initial states that exercise every possible scenario in time step 1: the mirror images 10111 and 11101 when surrounded by runs of dead cells.
Now I see only the one real stable rule: rule 204. 204 is binary 11001100, each bit of which is exactly the middle bit of numbers 7-0. In other words, every scenario maps to the central square.

Even here, though, the long runs of dead cells keep the "true nature" of a rule from coming out. I think random initial conditions do that much better.
Perhaps what would be best is to keep our simple pattern in the center exercising all scenarios, and then pad it with a random initial state. We do have to remember to pad it out with 3 dead cells. Let's do that on both sides for symmetry.
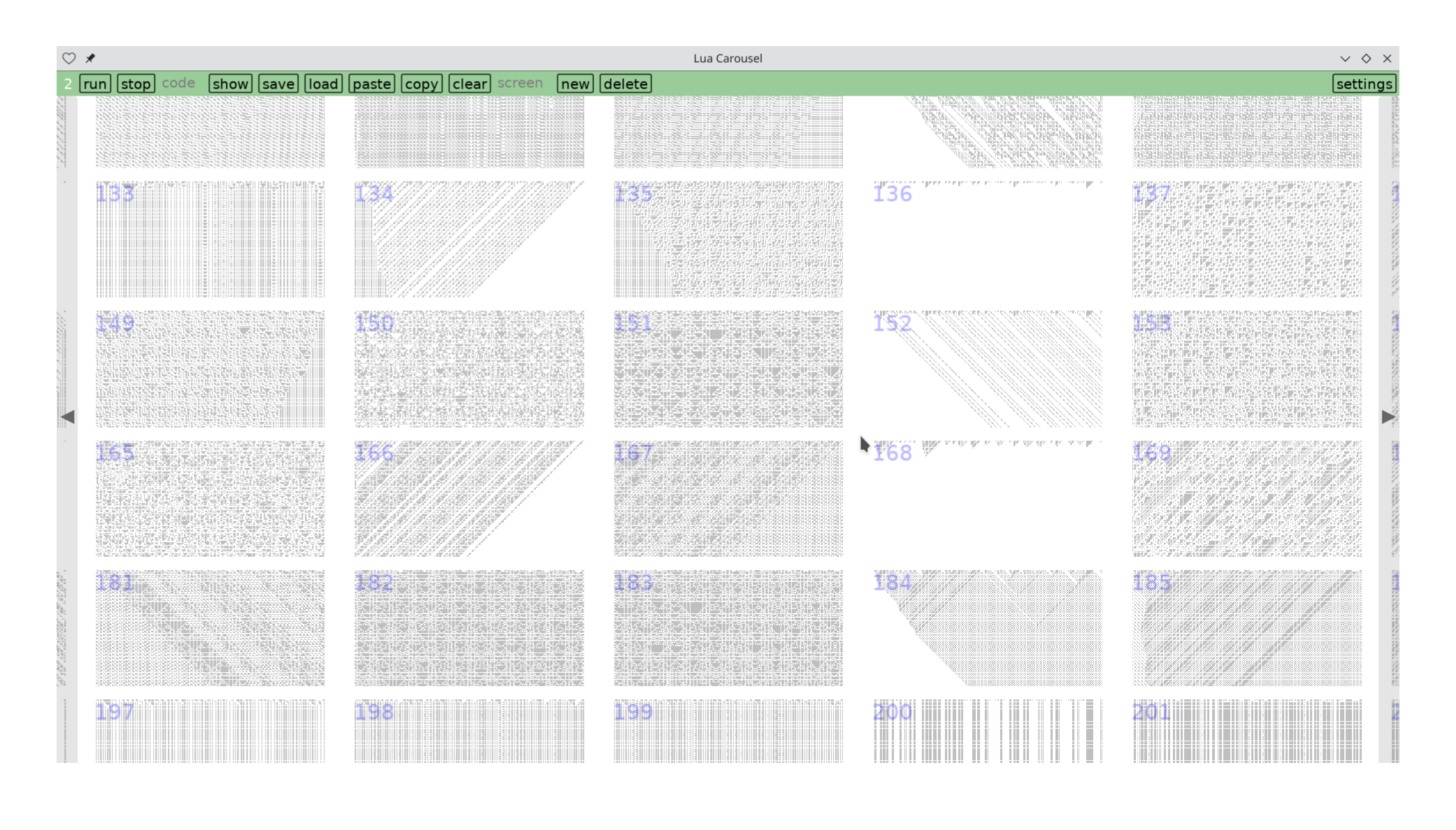
Ah, here's a nice screenshot of a central portion of the ruleset, ideal density for chaos to emerge.
Links
This post is part of my Freewheeling Apps Devlog.
Comments gratefully appreciated. Please send them to me by any method of your choice and I'll include them here.